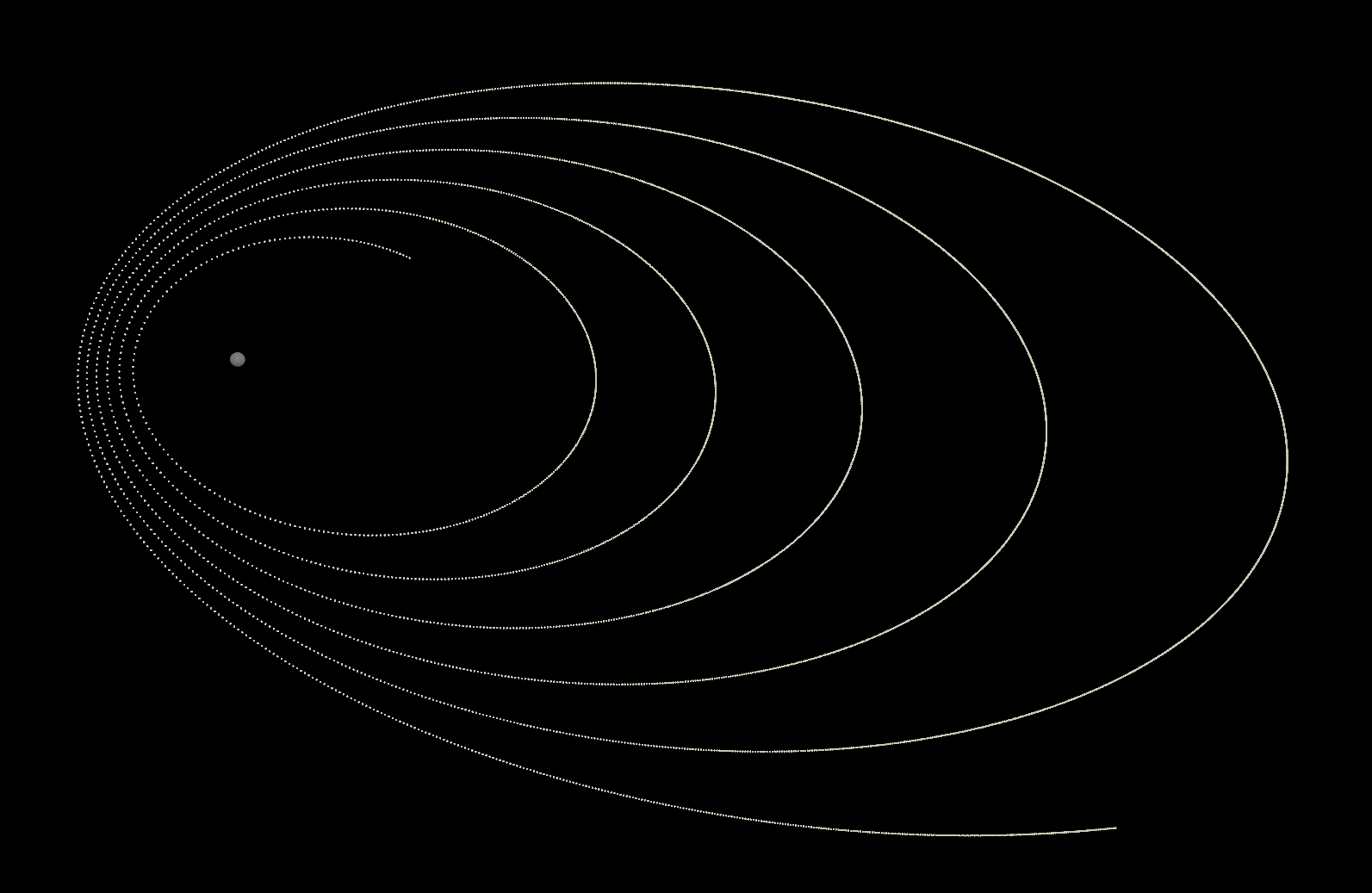
Point-Based Simulation (Simplified Newtonian Gravity)
To begin exploring gravitational interactions in Houdini, we provide a simplified Newtonian gravity simulation.
This setup computes pairwise forces between points, suitable for small systems or educational purposes.
int npts = npoints(0);
float G = 0.001;
vector g = {0,0,0};
for (int i = 0; i < npts; i++){
if (i == @ptnum) continue;
vector p1 = @P;
vector p2 = point(0, "P", i);
float m1 = @mass;
float m2 = point(0, "mass", i);
vector dir = normalize(p2 - p1);
float r = length(p2 - p1);
float acceleration = G * m1 * m2 / (r*r);
g += dir * acceleration;
}
@force = g;
@v *= 0.99;
Explanation:
G – gravitational constant (adjust for simulation scale)@P – current point’s position@mass – point mass- The loop calculates pairwise gravitational forces and stores the result in
@force.
@v *= 0.99; – damping to stabilize motion
For convenience, users can download and use the Houdini Digital Asset (HDA), which encapsulates this code and provides a ready-to-use interface.
Volumetric & Hybrid Gravity Simulation
For large-scale systems such as star formation or galactic evolution, point-based methods alone are computationally expensive.
We introduce a hybrid approach that combines point-based N-body simulations with volumetric gravity fields.
- Volumetric Gravity Fields: OpenVDB volumes represent matter density, enabling efficient computation in dense regions.
- Point Advection: Points representing stars or dust are advected within the volumetric fields to capture both large-scale and local interactions.
- Frame-by-Frame Field Generation: Gravity fields are recalculated each frame to reflect evolving mass distributions, improving accuracy over time.
- Hybrid Integration: Sparse regions use point-based N-body calculations, while dense regions leverage volumetric fields for efficiency.
This hybrid simulation allows efficient handling of billions of particles and produces high-quality data for further scientific analysis or cinematic rendering in the AMR project.
Implementation Notes: Houdini’s procedural framework and OpenVDB support are used to generate and advect volumetric fields.
Points follow the gradient of the density field each frame, allowing accurate simulation of emergent structures while maintaining computational efficiency.
Maya Python Alternative
Artists or researchers more comfortable with Maya can use a simplified Python script that computes Newtonian gravitational forces
between selected objects without volumetric fields. This approach is ideal for small-scale simulations or visual experimentation.
import maya.cmds as cmds
import maya.api.OpenMaya as om
def apply_gravity(objs, G=0.001):
positions = [om.MVector(*cmds.xform(o, q=True, ws=True, t=True)) for o in objs]
masses = [cmds.getAttr(o + ".scaleX") for o in objs] # using scale as proxy for mass
forces = [om.MVector(0,0,0) for _ in objs]
for i in range(len(objs)):
for j in range(i+1, len(objs)):
p1, p2 = positions[i], positions[j]
m1, m2 = masses[i], masses[j]
dir_vec = p2 - p1
dist = dir_vec.length()
if dist < 0.001: continue
force_mag = G * (m1 * m2) / (dist * dist)
f = dir_vec.normal() * force_mag
forces[i] += f
forces[j] -= f
for i, obj in enumerate(objs):
cmds.move(forces[i].x, forces[i].y, forces[i].z, obj, r=True)
objs = cmds.ls(sl=True)
apply_gravity(objs)
Tip: This script provides a quick way to simulate gravity in Maya, but for large-scale, hybrid simulations, Houdini is recommended.